The Black-Scholes model is a foundational element in our equity benchmarking data at Ravio.
It enables us to understand the value of equity compensation and to compare different types of equity (stock options, RSUs, phantom shares/virtual stock options etc) on an apples-to-apples basis
In this article we’ll explain:
- Why is equity compensation hard to benchmark?
- What is the Black-Scholes model?
- How does the Black-Scholes model work to calculate equity benchmarks?
Why is equity compensation so hard to benchmark?
Equity compensation is notoriously hard to compare across companies.
It can come in many different shapes and forms, especially in private companies.
This poses a challenge for companies like Ravio that provide equity insights sourced from a wide spectrum of companies using different types of equity, from early-stage startups all the way to large publicly-listed companies.
Here’s an example to illustrate why it’s so challenging to objectively compare equity compensation across different organisations.
Let’s say two companies are competing to hire a mid-level Software Engineering candidate:
Company A is a large public company with a current share price of $20. The company offers 3,000 RSUs to the Engineer, so the equity package has a market value of $60,000. Easy.
Company B is a fast-growing Series B startup (non public) whose shares were valued at $10.00 in the last funding round. The company offers 10,000 stock options to the Engineer at a strike price of $10.00.
How do we value this equity offer? Is it $10 share price 10,000 stock options = $100,000 or is it ($10 share price - $10 strike price) 10,000 stock options = $0?
The answer is neither.
Since company B is not publicly listed, its shares cannot be freely traded on the market like Company A’s shares. We have to make some assumptions about the expected future value of the shares, and then discount this back to the present day. Only then will a direct comparison between the two offers be possible*.
As you can see, the offers are very different – and we’ll pick this example back up at the end of the article to model out the fair market value of Company B’s stock.
So how do we deal with this for our equity benchmarks?
Well, for RSUs or other forms of straight equity, we use the simple fair market value at time of grant and flow that into our benchmarking results.
For stock options, virtual stock options, and warrants, we rely on the Black-Scholes model to enable an apples-to-apples comparison with RSUs.
Let’s dive into the specifics of how the Black-Scholes model works.
*Caveat: while this comparison works from a statistical and mathematical perspective, nobody can predict how each company will actually perform over time. Just because one equity package is higher on paper than another does not imply that it will actually turn out that way, so any candidate should always do thorough research to form their own opinion about the financial viability and upside potential of any company (in addition to factoring in other elements unrelated to compensation).
🤔 How do Ravio's equity benchmarks work?
Before we dive into the Black-Scholes model, a note about how Ravio’s equity benchmarks work…
The main figure we care about is the market value of each employee equity package at the time of grant – for the purpose of our benchmarks, it is irrelevant how the share price of each company evolves beyond that grant date.
The reason for this is simple.
Our customers use Ravio to inform their compensation decisions for new hires and existing employees. They need to understand how much the market (i.e. their peers and competitors) were willing to pay for talent at the time they granted each of their employee equity packages – whether that’s a new hire grant or a refresh grant. Whether these grants subsequently increase or decrease in value is less relevant.
What is the Black-Scholes model?
The Black-Scholes model (sometimes also known as the Black-Scholes-Merton model) is a mathematical model which enables the fair market value of share options to be calculated.
This includes company share options granted to employees as equity compensation, which is our focus at Ravio.
In very simple terms, the Black-Scholes model uses a standard normal probability distribution to account for the many variables which can impact the future value of shares.
It’s the most well-known and commonly used methodology for standardising equity benchmarks, and is typically seen as the industry standard – as well as being relatively simple to implement.
How does the Black-Scholes model work to calculate equity benchmarks?
Let’s take a closer look at how the Black-Scholes model actually works.
The six inputs of the Black-Scholes model
The Black-Scholes methodology uses six key inputs to model the future value of an option. The figure is then discounted to give the present value of the equity today.
As you can tell from this, the model does rely on assumptions and probability – so it’s not a prediction for how the future will play out. But, time has shown it to be a fairly reliable method, and it still enables that all-important comparison between stock options with different parameters.
The six inputs used are as follows.

1. Current share price
This is the market value per share of the company at the time of grant. It’s easy to determine this value for public companies (where typically the 30-day average share price is taken to determine equity grants). For private, i.e. non-public, companies, the market value per share is typically based on the most recent funding round or private transaction.
2. Strike price
The strike price (or exercise price) determines the price that the employee must pay to exercise their options. This impacts the market value because the lower the strike price, the higher the employee upside when selling the options.
The strike price is pre-agreed in the equity grant agreement between company and employee and does not change over time.
3. Option term (aka time to expiration)
Typically, stock options can be exercised and sold at any point from when they start vesting and their expiration date. For simplicity reasons, the Black-Scholes model assumes that the option can only be exercised at the end of its expiration date (i.e. a so-called “European option”).
As the time to expiration increases, the value of the option increases because there is more time for the stock price to move in a positive direction.
While expiration dates for stock options vary from company to company, we found that the vast majority of private tech companies use a standard 10 year expiration window for their stock options, which is why we also use 10 years as the standard assumption for our model. Some companies also include a post-termination exercise window to account for employees leaving a role, which can be as short as 90 days (e.g. in the case of EMI options in the UK where this is a legal requirement to preserve the tax beneficial status of the instrument).
For simplicity, any post-termination exercise requirements are not factored into our Black-Scholes calculations at Ravio.
4. Risk-free rate
The risk-free rate is simply the rate of return on a risk-free investment, such as a government bond. As the risk-free interest rate increases, the value of a stock option also increases.
Of course, the future interest rate is an unknown variable, even though historically it has tended to fluctuate within a relatively narrow band.
Ravio uses a weighted average 10-year bond yield for a basket of different government bonds (~3.5%).
5. Volatility
Volatility measures the degree of variation of a stock's price over time. Higher volatility increases the likelihood that the stock price will move significantly, making options more valuable (aka upside). The Black-Scholes model assumes that volatility remains constant over the life of the option.
While volatility is impossible to predict with certainty, it’s generally more likely that volatility will be higher for early-stage companies and decrease over time as the business matures.
At Ravio, we use different volatility assumptions based on the funding/maturity stage of a company. For public companies, we use the historical volatility of the stock price.
6. Dividend yield
Some companies pay dividends to shareholders as a way to share profits with their shareholders, either in the form of cash payouts or additional shares granted in the company.
Since the vast majority of companies using Ravio do not pay dividends, and dividends tend to only have a minor effect on the fair market value of options, we assume no dividends are paid for the purposes of calculating equity benchmarks at Ravio.
The Black-Scholes formula
So what’s the actual calculation used for the Black-Scholes model?
Here it is:
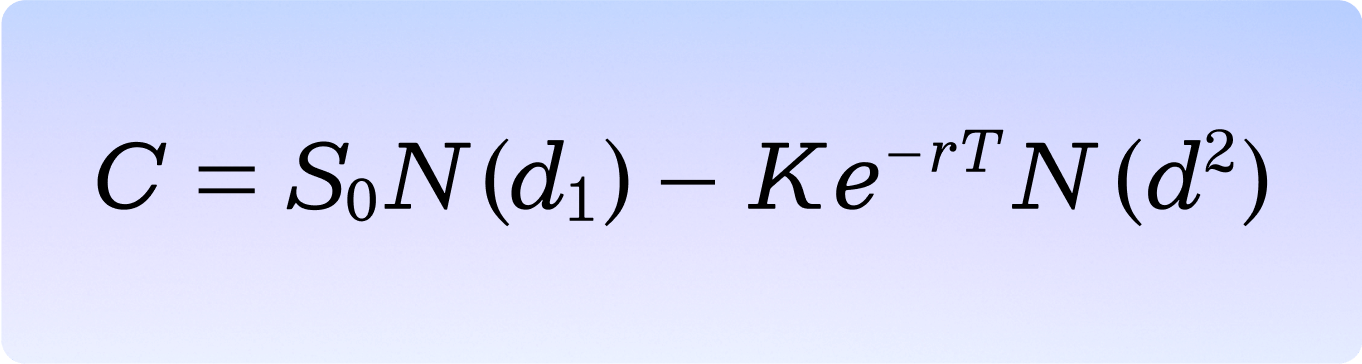
The formula first looks at the likely amount of money that will be received by selling the share options – this is S₀N(d1), where S is the current share price and N(d1) is a statistical variable which accounts for the probability that the stock will be ‘in the money’ at the time of sale i.e. the share price is greater than the strike price.
Then the likely amount of money that will be paid to buy the shares in order to sell them is subtracted from this – this is Ke⁻ʳᵗ N(d2), where K is the strike price, r is the risk-free rate, t is the expected term, and N(d2) is a statistical variable which accounts for the probability that the shares will be exercised at all.
The difference between these two expressions gives us C, which is the fair market value of the equity package.
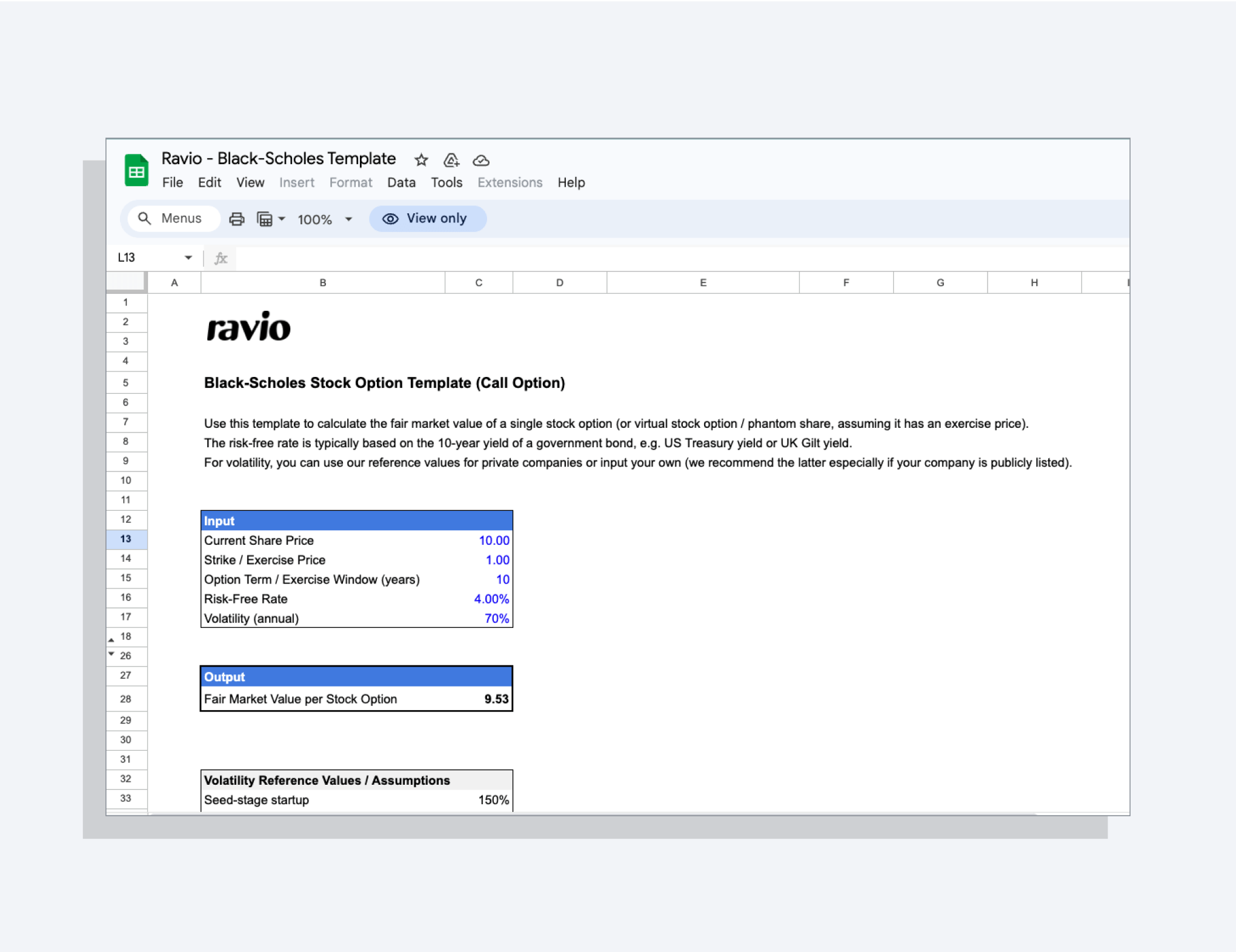
If you’re interested in exploring the fair market value for your equity compensation or modelling different outcomes, make a copy of our Black-Scholes calculator template ⬇️
Translating the fair market value into a new hire equity grant benchmark
We use the standardised fair market value which is the output of the Black-Scholes foruma as the basis of our equity benchmarks.
Each company that uses Ravio also inputs their unique approach: their latest company valuation, current share price, strike price, chosen vesting schedule.
This enables us to then translate that fair market value into the typical new hire equity grant for those parameters, giving you the relevant equity benchmarking data for your specific company – which is shown to you in two ways in our platform:
- Percentage ownership (%) for early-stage companies (pre-seed and seed)
- Grant value in absolute terms (£) as well as % of base salary for Series A companies and beyond
This is to reflect the reality in most tech companies, with business leaders typically thinking in terms of equity ownership at the early stages of a company, and then shifting to thinking in terms of absolute financial terms at the later stages.
To wrap things up, let’s close the loop and go back to our earlier example in the first part of this article, of Company B who is competing with Company A for a Software Engineering candidate and offers 10,000 stock options to the Engineer at a strike price of $10.00.
Using the previously described Black-Scholes model and using the assumptions outlined above, the fair market value of Company B’s offer turns out to be $90,483. You can see the exact calculation per stock option in our template.
This is ~50% higher than Company A’s offer of 3,000 RSUs at a share price of $20, so it’s a comparatively strong equity offer.
But will our Software Engineering candidate actually use Black-Scholes to price the offer? Or will they apply a huge discount because the shares are not liquid and carry more risk than those of Company A?
How candidates evaluate and compare equity compensation offers, especially when comparing between public and private companies, is a separate (and fascinating!) topic – which we’ll cover in a future article.



